The stability of an elastic plate in axial incompressible subsonic flow has been studied by several scholars, beginning in 1968 with experimental observations of a flapping flag by Taneda. Flutter is a specific dynamic instability of a structure in a moving fluid that exhibits unsteady and large oscillations due to the interaction between the structure and the fluid. Historically, the majority of flutter research has been focused on suppressing flutter because it is catastrophic in many structures including aircraft, bridges, and turbomachinery. Recently, attention has been refocused to gain a better understanding of flutter due to a growing interest in small scale energy harvesting systems. Even though attention has been refocused there remain significant differences between existing theoretical predictions and experimental observations.
We have created a theory and code that models the three dimensional aerodynamic forces acting on a structure which is modeled with energy methods using modal coordinates. We determine the modal coordinates either analytically or, for more complicated geometries, using finite element methods. We model the aerodynamics using a Vortex Lattice Model (VLM) which captures the forces created by a three-dimensional, incompressible flow by tracking the motion and the strengths of a set of horseshoe vorcitices which are solutions to the governing potential flow equation. We then solve the coupled aeroelastic equations in the frequency domain and track how the modal damping and frequency for a desired configuration change with the wind conditions.
Yawed Flow
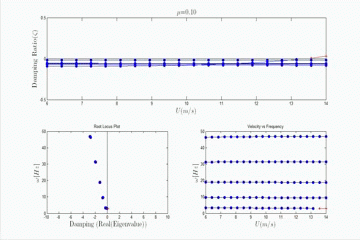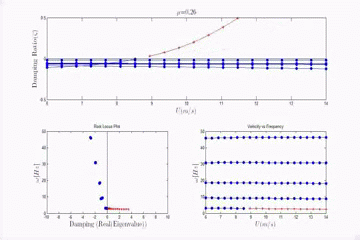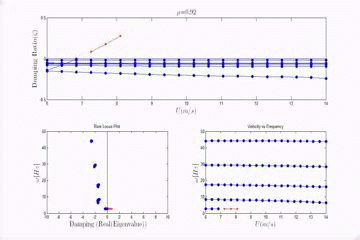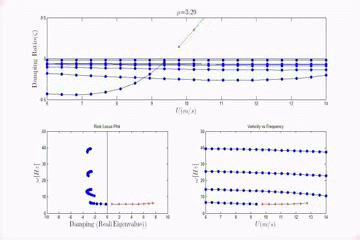
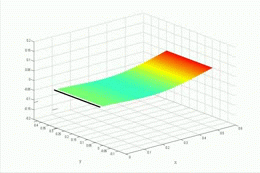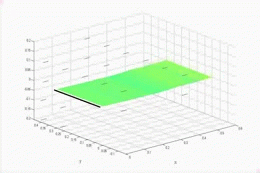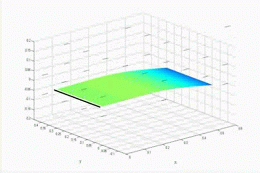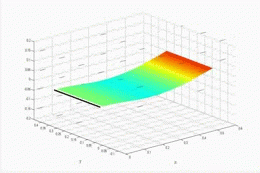
In addition to exploring the flapping flag configuration, we have also explored the transition between flag flutter, and wing-like flutter, a classical flutter type that arises when the clamped edge of the plate is aligned with flow direction. The aeroelastic stability is determined in the frequency domain and the flutter boundary is explored as the plate is rotated from the clamped edge normal to the flow configuration (0 degrees) to the clamped edge aligned with the flow (90 degrees). The angle of the transition from flag to wing-like flutter is dependent on the relative spacing of the first torsion and second bending natural frequencies from the first bending natural frequencies. Aeroelastic simulations predict that the closer the first torsion frequency is to the first bending frequency, the closer to the flag configuration that the flutter transition occurs. The animation to the right shows the evolution of the aeroelastic eigenvalues as the yaw angle changes from 0 to 90.
Experiments
This research project leverages the capabilities of the Duke University Wind Tunnel. The theoretical models are validated with experimental tests. The videos below show two examples of different flapping flag structures that were tested in the wind tunnel.