For the past two decades the Volterra series has been successfully utilized for the purpose of flutter prediction, aeroelastic control design and aeroelastic design optimization. The approach has been less successful however, when applied to other important aeroelastic phenomenon such as aerodynamically induced limit cycle oscillations. Similarly to the Taylor series, the Volterra series is a polynomial based approach capable of progressively approximating nonlinear behavior using an infinite summation of quadratic, cubic, and higher-order functional expansions. Unlike the Taylor series however, kernels of the Volterra series are multi-dimensional convolution integrals that are computationally expensive to identify. Thus, even though it is well known that aerodynamic nonlinearities are poorly approximated by quadratic Volterra series models, cubic and higher-order Volterra series truncations can not be identified because their identification costs are too high. We explore a novel, sparse representation of the Volterra series whose identification costs are significantly lower than the identification costs of the full Volterra series. We demonstrate that sparse Volterra reduced-order models are capable of efficiently modeling aerodynamically induced limit cycle oscillations of the prototypical NACA 0012 benchmark model. These results demonstrate for the first time that Volterra series models are capable of modeling aerodynamically induced limit cycle oscillations.
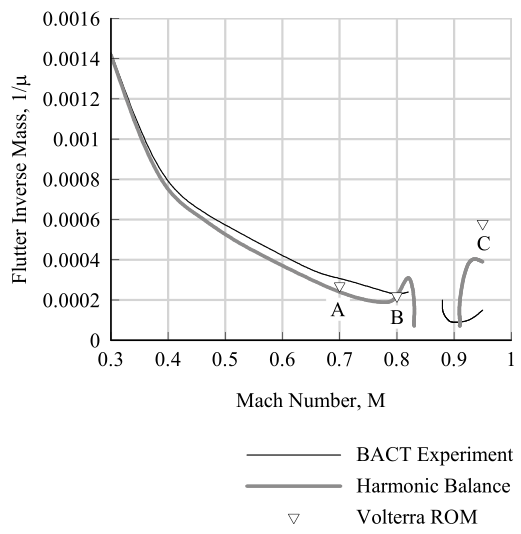
Figure 1. NACA0012 benchmark model flutter boundary.
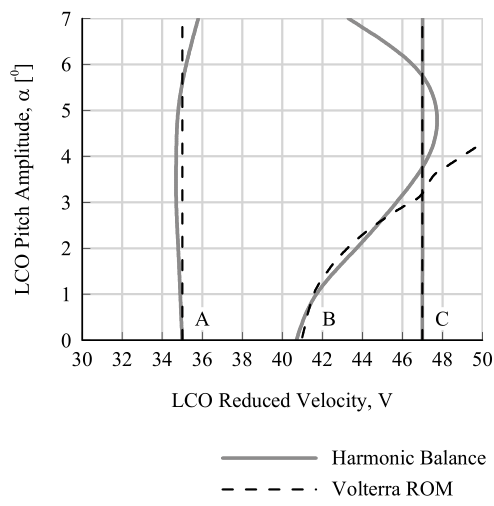
Figure 2. NACA0012 benchmark model LCO amplitude.