Turbulence is a phenomenon characterized by chaotic, multi-scale dynamics, both, in space and time. At high Reynolds numbers, the dynamics of turbulence exhibit an energy cascade: large scale eddies are broken down into smaller and smaller eddies until the scales are fine enough so that viscous forces can dissipate their energy. We generalize the POD-based Galerkin model order reduction approach by incorporating Navier-Stokes equation constraints. In this method, the derived Galerkin expansion minimizes the residual like POD but with the power balance equation for the resolved turbulent kinetic energy as an additional optimization constraint. Thus, the projection of the Navier-Stokes equation onto the expansion modes yields a Galerkin system which respects the power balance on the attractor. The resulting dynamical system requires no stabilizing eddy-viscosity term - contrary to other POD models of high Reynolds number flows.
Figure 2 illustrates the evolution of the turbulent kinetic energy E(t) inside a square two-dimensional lid-driven cavity at Re = 30 000. The grey line corresponds to a fully resolved pseudo-spectral Direct Numerical Simulation (DNS). The dashed line corresponds to a standard POD-based Galerkin ROM utilizing the first n = 20 most energetic POD basis functions. The red line corresponds to a n = 20 Galerkin ROM derived using the proposed new methodology. Figure 3 illustrates the evolution of the turbulent kinetic energy of a two-dimensional, quasi-incompressible (M = 0.033) mixing layer at Re = 500 based on initial vorticity thickness.
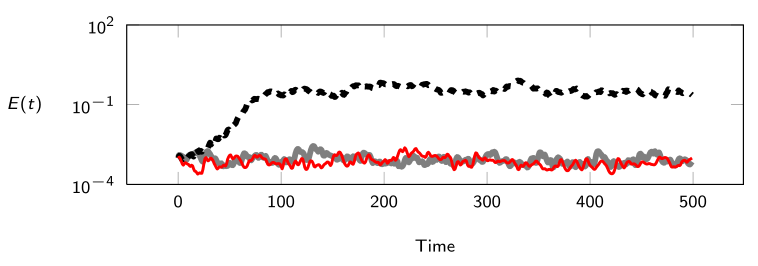
Figure 2. Time evolution of the turbulent kinetic energy inside a square two-dimensional lid-driven cavity at Re = 30 000; CFD (grey line) standard POD-based Galerkin ROM (dashed line) the new Galerkin ROM (red line).
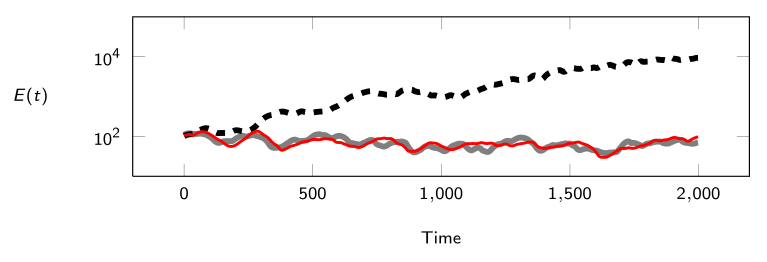
Figure 3. Time evolution of the turbulent kinetic energy of a two-dimensional, quasi-incompressible mixing layer at Re = 500; CFD (grey lines) standard POD-based Galerkin ROM (dashed line) the new Galerkin ROM (red line).
Additional Details
- Balajewicz, M., Dowell, E.H., Noack B., (2012) "Model order reduction of the navier-stokes equations at high reynolds number." American Physics Society Presentation