The proper orthogonal decomposition (POD) is modal basis construction technique which was arguably first introduced to the problem of turbulence by J.L. Lumley in 1967. The reader is directed to an Annual Review on this topic for a brief mathematical and historical overview. The general principle is to reproduce a signal u(x,t) using a finite sum of orthonormal eigenvalue-eigenvector pairs
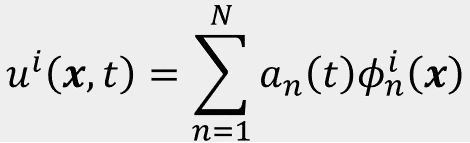
such that the signal is reproduced using only its dominant coherent structures. The POD modes are found by identifying the linear basis which optimally, in the mean L2 sense, spans the subspace of the signal.
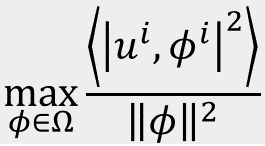
If the provided signal u(x,t) is a velocity function, then the POD modes optimally capture the flow’s mean kinetic energy, viz. the mean of the signal squared. However, the kinetic energy is not the only important function of the velocity in a turbulent fluid flow. In fact, it is representative of only the largest scales of motion; turbulence by definition is governed by dynamics as a spectrum of spatial scales, with all dissipation occurring at the smallest of scales. Without accurate inclusion of coherent structures (viz. modes) at all scales, the modal basis will not accurately span the system’s dynamics even if it does span the provided signal. This is apparent from the unpredictable success of POD-based reduced-order models (ROMs).
Another concern with applying POD-based ROMs of to turbulent fluid flows is that there is no a priori uncertainty quantification that can be extracted from the modal basis construction. In other words, it is not clear how well a particular truncated modal basis captures the system’s multiscale dynamics until the ROM is tested. With such low confidence on the modal basis’ dynamical accuracy, it is thus difficult to apply the ROMs for engineering purposes including parametric extrapolation.
Several approaches have been developed in which the nature of the POD’s optimality is manipulated to yield modal bases which are potentially more dynamically intuitive than are the classic POD modes. Some of these methods involve adjustments to the first equation above; others involve adjustments to the second.