The 2D regularized lid-driven cavity is a canonical internal fluid flow problem in which fluid convects in a sealed box as driven by a moving lid. The boundary conditions are as follows.
Image
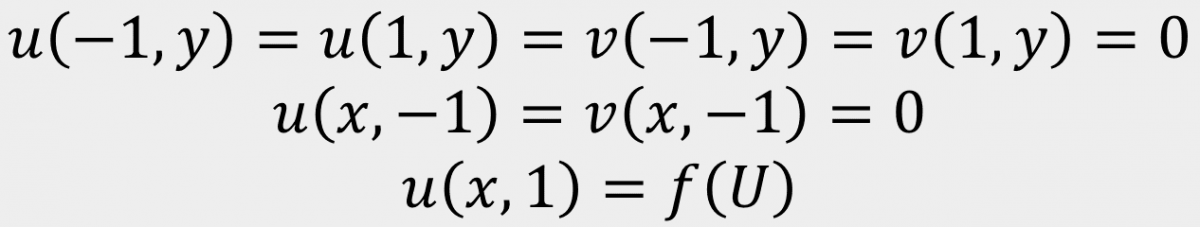
The system is known to qualitatively change as the Reynolds number increases. High-fidelity simulations of the system presented a Hopf bifurcation near Re = 10,250 and a toroidal bifurcation near Re = 15,500 with a slow progression to chaos at higher Reynolds numbers. These bifurcations were observed through both Poincaré sections and power spectra.
Image
Image
Image
Image
Image
Image
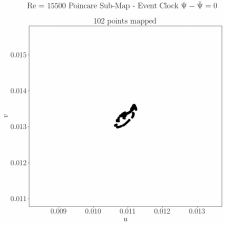
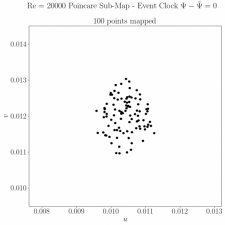
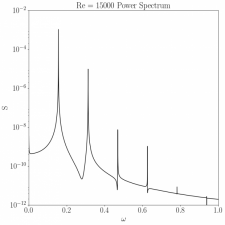
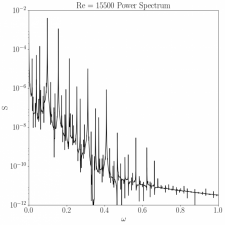
This research, summarized in a recent publication, identified patterns in the nature of the bifurcations. The potential for bifurcation prediction was established and is a focus of current research.